epsilon-约束方法

发表于 阅读次数： 本文字数： 4.2k 阅读时长 ≈ 8 分钟
epsilon-约束方法是一种多目标优化算法，借助它我们也可以使用Gurobi等求解工具求解多目标优化算法，且其求解效果比加权法更好。

$\varepsilon$-约束方法（这样GUROBI也能解多目标问题了！）

一般解决多目标优化问题的算法都是NSGA-II算法、MOEA-D算法等多目标智能算法。采用Gurobi精确求解的方法往往难以求出pareto最优解，只能通过对多个目标进行加权的方式求解。今天我们学习一种方法，借助它我们也可以使用Gurobi等求解工具求解多目标优化算法，且其求解效果比加权法更好。

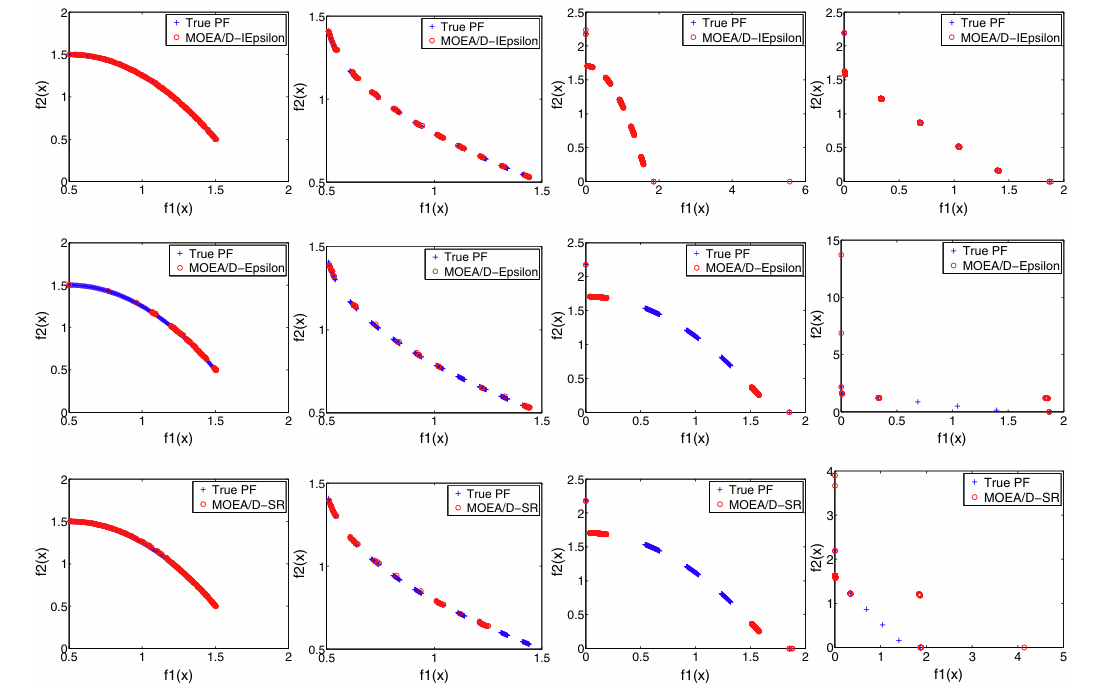
$\varepsilon$-约束方法简介

$\varepsilon$-约束方法是一种多目标优化算法。它基于约束优化的思想，通过引入一个参数$\varepsilon$来控制目标函数的权重，从而保证满足约束条件的前提下，寻找到最优解的近似解集。

通过选取一个主目标函数，将其余目标函数转化为约束，从而计算每个子优化目标，得到帕累托解集。

过程

针对一个多目标优化问题：
$$
min {f_1(x),f_2(x),f_3(x)} \
h(x)=0 \
g(x)\leq 0
$$

使用ε约束算法转化问题为：
$$
min f_1(x) \
f_2(x)\leq \epsilon_2,\cdots,f_n(x)\leq\epsilon_n \
h(x) = 0 \
g(x) \leq 0
$$
其中的每个参数$\epsilon_2,\epsilon_3,\cdots,\epsilon_n$通过计算payoff矩阵得到。

payoff的计算过程：

  1. 求解出第i个目标函数的最优值$f_i(x_i^*)$，得到其最优解$x_i^*$；

  2. 将$x_i^*$代入其他目标函数得到${f_1(x_i^*),f_2(x_i^*),\cdots,f_n(x_i^*)}$；

  3. 对全部目标函数按照上述流程求解，得到payoff table矩阵如下：
    $$
    \begin{bmatrix}
    f_1(x_1^*) & \cdots & f_i(x_1^*) &\cdots & f_n(x_1^*)\
    \vdots& \ddots &&& \vdots\
    f_1(x_i^*) & \cdots & f_i(x_i^*) &\cdots & f_n(x_i^*)\
    \vdots& \ddots& & & \vdots \
    f_1(x_n^*) & \cdots & f_i(x_n^*) &\cdots & f_n(x_n^*)\
    \end{bmatrix}
    $$

该方法本质上与网格搜索法相同。得到了payoff矩阵之后，可以求出每个目标的最优值和最劣值（就是每个目标维度的最大和最小值）。记为最优解(U)和最劣解(SN)$f_i^U = f_i(x_i^*)$,$f_i^{SN} = f_i(x_j^*)$。

选择一个主目标函数$f_k(x)$。

对于主目标函数外的目标函数$f_{i}(x)$，设置一个网格化分数$q_{ij}∈{1,2,\cdots,q_i,max} $。

由此计算除了主目标函数外的其余目标函数的ε约束如下：
$$
ϵ_{ij}=f_i^{SN}−\frac{(f_i^{SN}−f_i^{U})}{q_{ij}}⋅j \qquad j=1,2,…,q_{i,max}
$$
得到每个优化子问题如下：
$$
min f_k(x)\
s.t. \qquad f_1(x)\leq \epsilon_{1j},f_2(x)\leq \epsilon_{1l},f_n(x)\leq \epsilon_{1m},h(x)=0,g(x)\leq0
$$
其中,$j=1,2,\cdots,q_{1,max};l=1,2,\cdots,q_{2,max};\cdots;m=1,2,\cdots,q_{n,max};$

每次求出一个最优解，若在可行域内则加入帕累托解集，若不在可行域内则丢弃。

例子

$$
min \quad f_1(x) = x_2-x_1 \
min \quad f_2(x) = x_1+x_2 \
s.t. \qquad x_1^2 - 2x_1 + 1 \leq x_2 \
0 \leq x_1 \leq 1 \
0 \leq x_2 \leq 1
$$

使用python+gurobi求解代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2024/3/3 11:35
# @Author  : TUUG
# @Email   : tr6666666@qq.com
import numpy as np
from matplotlib import pyplot as plt
import gurobipy as gp

def f1(constraint=None):
    model = gp.Model()
    x1 = model.addVar(name="X1",vtype=gp.GRB.CONTINUOUS,lb=0,ub=1)
    x2 = model.addVar(name="X2",vtype=gp.GRB.CONTINUOUS,lb=0,ub=1)
    # 添加约束
    model.addConstr(x1*x1-2*x1+1<=x2)
    if constraint is not None:
        model.addConstr(x1+x2<=constraint)
    # 定义目标函数
    model.setObjective(x2-x1, sense = gp.GRB.MINIMIZE)
    model.update()
    # 求解模型
    model.optimize()
    return x1.x,x2.x
    
def f2():
    # 创建模型
    m2 = gp.Model("f2_optimization")
    # 定义变量
    x1 = m2.addVar(name="X1",vtype=gp.GRB.CONTINUOUS,lb=0,ub=1)
    x2 = m2.addVar(name="X2",vtype=gp.GRB.CONTINUOUS,lb=0,ub=1)
    # 添加约束
    m2.addConstr(x1*x1-2*x1+1<=x2)
    # model.addConstr(x2-x1>=cons)
    # 定义目标函数
    m2.setObjective(x2+x1, sense = gp.GRB.MINIMIZE)
    # 求解模型
    m2.optimize()
    return x1.x,x2.x

f11,f12 = f1()
f21,f22 = f2()
f1_min = f12-f11
f2_max = f11+f12
f2_min = f21+f22
f1_max = f22-f21
print('--------------')
print(f2_min,f2_max)
soultion_pool = []
q_n =10
for q in range(q_n):
    constraint = f2_max-(f2_max-f2_min)/q_n*q
    # constraint = np.linspace(f2_min,f2_max,10)[q]
    f11,f12 = f1(constraint=constraint)
    soultion_pool.append([f12-f11,f11+f12])
print(soultion_pool)

import numpy as np
import matplotlib.pyplot as plt
pareto_front_solutions = np.array(soultion_pool)

# 绘制 Pareto 前沿解
plt.scatter(pareto_front_solutions[:, 0], pareto_front_solutions[:, 1], label='Pareto Front')
plt.xlabel('f1(x)')
plt.ylabel('f2(x)')
plt.title('Pareto Front for Multi-objective Optimization')
plt.legend()
plt.show()

求解结果展示如下

网格化分数取10时：

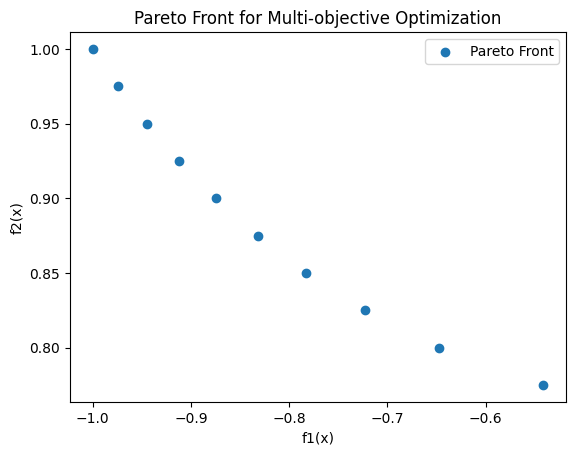
网格化分数取20时：

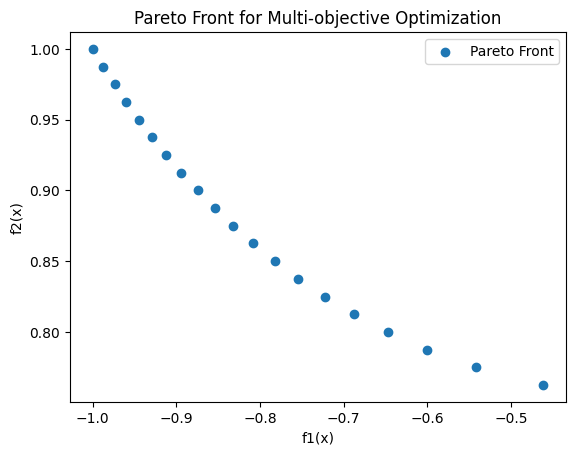
网格化分数取100时：

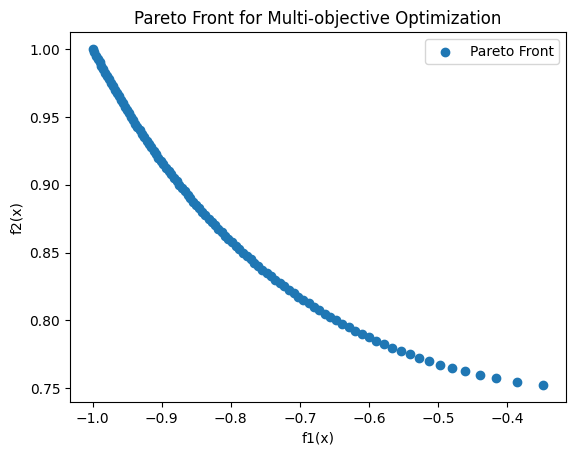
可以看到，这个方法有一个很好的性质，就是可以通过增大网格化分数来改善求解结果，使其更接近真实帕累托前沿。如果求解时间过长可以减小网格化分数来缩短求解时间。

参考文献

[1] Ismail-Yahaya A, Messac A. Effective generation of the Pareto frontier using the normal constraint method[C]//40th AIAA Aerospace Sciences Meeting & Exhibit. 2002: 178.

[2] Fan Z, Li W, Cai X, et al. An improved epsilon constraint-handling method in MOEA/D for CMOPs with large infeasible regions[J]. Soft Computing, 2019, 23: 12491-12510.

[3] Yang Z, Cai X, Fan Z. Epsilon constrained method for constrained multi-objective optimization problems: some preliminary results[C]//Proceedings of the companion publication of the 2014 annual conference on genetic and evolutionary computation. 2014: 1181-1186.

[4] 【多目标规划问题求解】ε-约束算法_约束法多目标规划问题求解-CSDN博客