针对共享出行系统的众包与地理围栏机制
[TOC]
基本信息
标题 : Beyond Repositioning: Crowd-Sourcing and Geo-Fencing for Shared-Mobility Systems
期刊 : Production and Operations Management (UTD24)
作者 :南方科技大学,何翘楚(研究运营管理和运筹学在智慧城市/可持续发展/人工智能等领域的应用)
发表时间 :2021
研究背景
共享单车平台的成功在很大程度上取决于它是否有盈利能力的以及满足通勤者不断变化的需求的能力。
共享单车平台的运营机制主要包括repositioning(依赖专职工作人员或车辆的调度策略),这篇文章提出了另一种机制——众包。
众包:通过用户奖励机制,激励用户主动参与车辆调度。
地理围栏:通过虚拟停车区域管理车辆分布,提高停车效率和城市空间利用率。
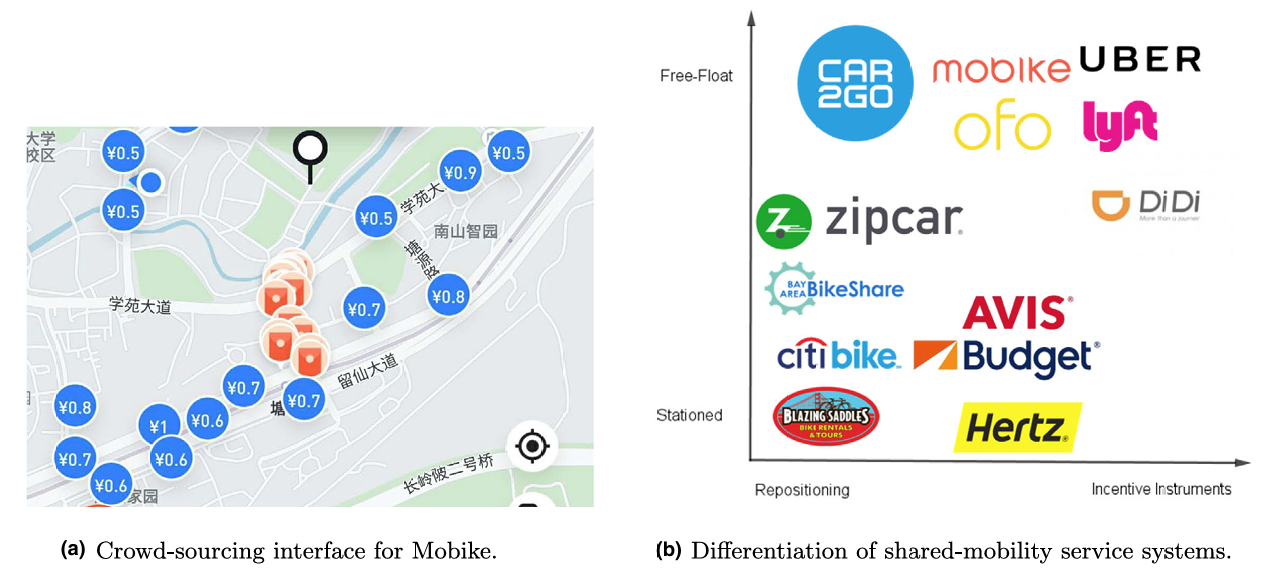
共享单车平台根据其特点可分为:站点到站点,自由浮动。该文主要针对的是图中靠近右上角的这些平台的运营场景。
提出问题
- 如何刻画市场的动态性与评价共享单车系统的表现?如何通过最优化激励和空间容量分配来保证平台的高服务水平、低运营成本、高容量利用率。
- 利用“众包”和“地理围栏”技术运营共享单车平台,可能的政策导向和管理见解?
文章贡献
- 文章提出了将众包(Crowd-Sourcing)和地理围栏(Geo-Fencing)技术结合到共享出行系统的设计中,替代了高成本的传统重定位(repositioning)策略,在共享出行系统中实现低成本的供需平衡。
- 文章提出了一种随机模型与重负载近似相结合的分析框架,用于优化自由浮动共享出行系统的设计与运营。可在不确定性条件下提供卓越的系统性能。
- 利用某个头部企业的真实行业数据,文章在自由浮动单车共享系统中验证了模型假设,并通过案例研究展示了模型在实际运营中的适用性。在多个约束条件下实现服务水平、成本和容量利用率的平衡。系统性能评估:对比不同近似方法的准确性和效率。
- 文章为共享出行平台和政策制定者提供了管理见解。市场厚度管理:通过精细的容量分配提升市场厚度。供需动态优化:适当的额外容量和激励机制可以显著改善供需匹配效率。策略比较:量化了众包和传统重定位策略在不同情境下的优势。
数学模型
模型介绍
针对一个城市,将其划分为$n$个区域,每个区域的出行价格$p_i$与奖励$r_i$都不同。
某个区域$i$的单车需求量随价格线性下降:$d_i = \lambda_i - \alpha_i p_i, \quad \forall i \in I.$
某个区域$i$的单车供应量随奖励线性上升:$s_i = \mu_i + \beta_i r_i, \quad \forall i \in I.$
价格$p_i$和奖励$r_i$可以为正也可以为负,这使得平台能够进行空间价格歧视。例如,从区域$i$到区域$j$的一次行程中,用户向平台支付的总费用为$p_i-r_j$。
在每个区域中,有一个固定分配的容量$N_i$,代表车辆的停车空间。过大的容量会侵占了公共空间。因此,在政府干预下,平台会限制不同区域内的单车最大数量$N_i$。
市场厚度(market thickness):当前时刻下,用户可以使用的车辆数。
双向队列:需求与供应的数量都是服从随机过程的。使用$n_i(t)$表示供应与需求在时刻$t$的差。
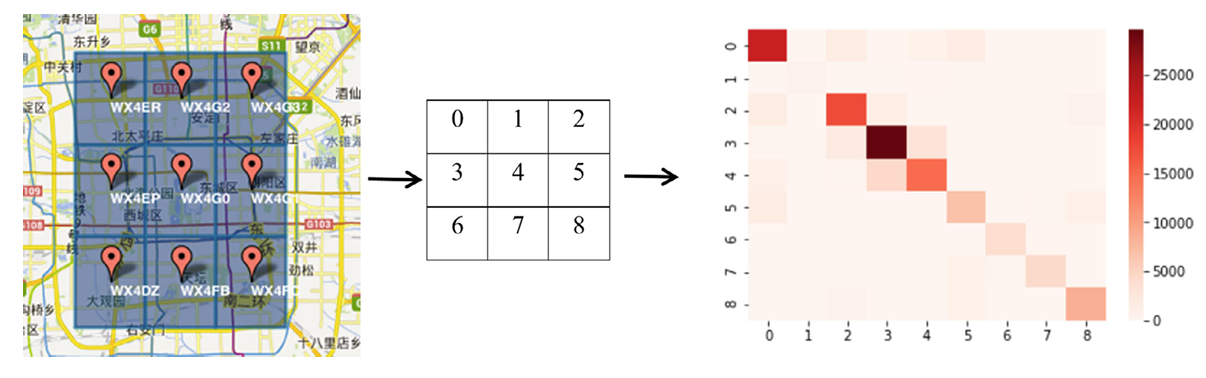
网络流假设:文章认为该问题不需要建模为一个网络流问题,因为根据北京市的出行数据,大多数情况下共享单车的行程距离不会超过1英里。OD矩阵具有明显的对角线占优特性,即非对角线元素几乎可以忽略不计。这也解释了为什么我们关注的是区域内的市场动态,而不是跨区域的网络交通流。
平稳性假设:在短时间内,需求与供应的到达可以看作是平稳泊松过程。我们还假设供需匹配是即时的。
模型分析
引理1:$n_i(t)$的稳态分布(根据马尔科夫稳态方程推导,流入等于流出)
$$\pi_x = \left( \frac{s_i - d_i}{s_i} \right) \left( \frac{d_i}{s_i} \right)^{N_i + x}$$
市场厚度为:(计算期望,利用几何级数公式结合求导可以推得)
$$L_i = N_i - \frac{d_i}{s_i - d_i} \left[ 1 - \left( \frac{d_i}{s_i} \right)^{N_i} \right]$$
任意一个顾客的等待时间为
$$W_i’ = \frac{1}{s_i - d_i} \left( \frac{d_i}{s_i} \right)^{N_i}$$
引理2:平台的长期稳态收益率如下:
$$
\Pi = \sum_{i \in I} p_i \cdot d_i - r_i s_i \lim_{t \to \infty} \Pr{n_i(t) \geq -N_i} \
= \sum_{i \in I} (p_i - r_i)(\lambda_i - \alpha_i p_i).
$$
考虑服务水平约束,以确保客户的预期等待时间满足以下条件:
$W_i^{\prime} = \frac{1}{s_i - d_i} \left( \frac{d_i}{s_i} \right)^{N_i} \leq T_i$
平台的决策问题建模如下:
$$
\begin{align*}
\max_{(p_i, r_i, N_i){i \in I}} \quad & \Pi = \sum{i \in I} (p_i - r_i)(\lambda_i - \alpha_i p_i), \
\text{subject to} \quad & \lambda_i - \alpha_i p_i < \mu_i + \beta_i r_i, \quad \forall i \in I, \
& \frac{\left( \frac{\lambda - \alpha_i p_i}{\mu_i + \beta_i r_i} \right)^{N_i}}{\mu_i + \beta_i r_i - \lambda_i + \alpha_i p_i} \leq T_i, \quad \forall i \in I, \
& \sum_{i \in I} N_i \leq N, \
& p_i, r_i \in \mathbb{R}, N_i \in \mathbb{Z}_+, \quad \forall i \in I.
\end{align*}
$$
目标函数为最大化平台的长期运营收益;约束1保证任意区域的需求量小于供给量;约束2保证了客户服务水平,这里的客户服务水平通过等待时间来衡量;约束3保证了所有区域的共享单车总数小于总的共享单车数量。
可以看出,服务水平约束是非线性。
命题1 当只有1个区域时,上述问题等价为这个问题:
$$
\begin{aligned}
& \min_{d_{i}, s_{i}} \prod_{i} \triangleq (ad_{i} + bs_{i} - c) d_{i}, \
\text{s.t. } & \
& d_{i}^N + T(d_{i} - s_{i})s_{i}^N = 0, \
& d_{i} \geq 0, \
& s_{i} \geq 0, \quad s_{i} \leq s_{i}^*,
\end{aligned}
$$
近似公式
文章探讨了不同形式的近似公式,以便获得分析结果和管理见解。系统性能在很大程度上取决于两个维度,即交通状态和市场厚度。文章主要针对三种情况下的近似公式进行了分析。$s_i = d_i + \delta \sqrt{d_i}$
低容量状态:即$N_i$可以忽略不计,此时服务水平约束变成:
$$
W_0 \approx \frac{1}{(s_i-d_i)} = \frac{1}{\mu_i + \beta_i r_i - \lambda_i - \alpha_i p_i} \leq T_i
$$
Capacity-independent 近似:系统性能与容量分配无关,特别是在高流量情况下,系统的性能主要由需求和供应相对强度决定,而不是由容量决定。
Capacity-dependent近似:这个部分认为系统性能受到分配的空间容量影响。
容量独立近似(应该是指所有的区域的共享单车容量互不相同的情况):
引理3:假设$ \delta^2 < \frac{1}{T_i N_i e} $且$N_i$较大,$\forall i \in I$。在容量相关近似下,服务水平约束 可以近似为: $$ W_i^{\prime}\approx \frac{1}{\delta \sqrt{d_i}+N_i \delta^2} \leq T_i, \forall i \in I $$
此时模型变为:
比较近似精度
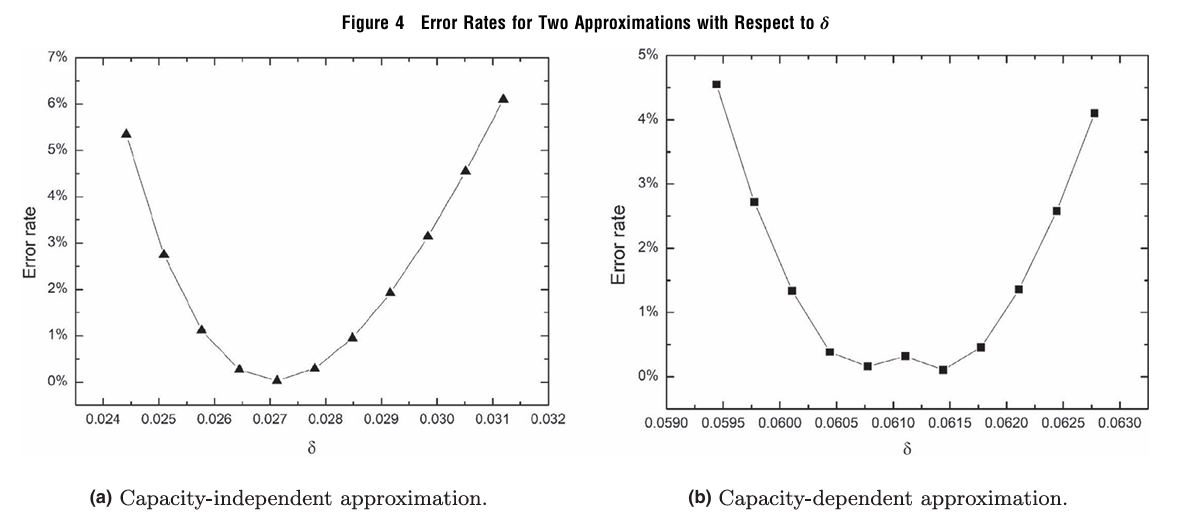
求解原始问题得到的解作为基准与两种近似模型进行对比。
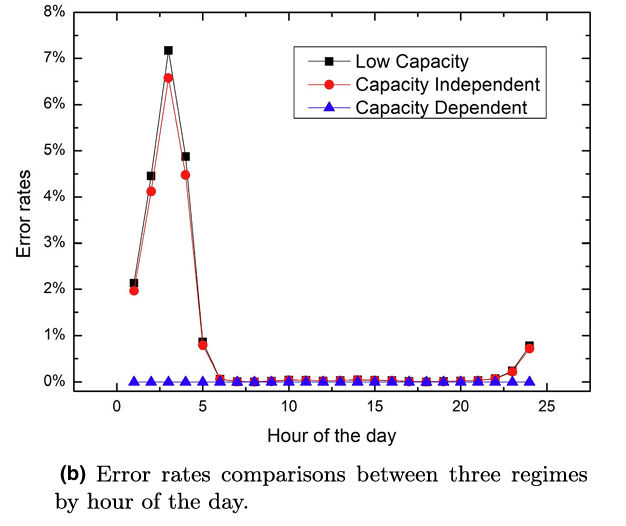
两种容量近似方法都对这种额外容量非常敏感。好消息是,容量相关近似对激励因素非常鲁棒。在白天,三种近似方法都很准确,而只有容量独立近似在深夜和清晨能够达到优秀的解决方案质量。这也表明,在低周转率的时段,容量管理显得尤为重要。
案例研究
利润比较揭示,系统的盈利能力对激励的调整程度非常敏感。
数据集来源于某个头部共享单车企业,文章首先将城市划分为100个区域,并计算每个区域的需求和供应率。
区域容量、运营成本、车辆利用率三者之间的关系。在图7a中,运营成本随着区域容量的增加而减少,而在图7b中,车辆利用率也随着区域容量的增加而减少。
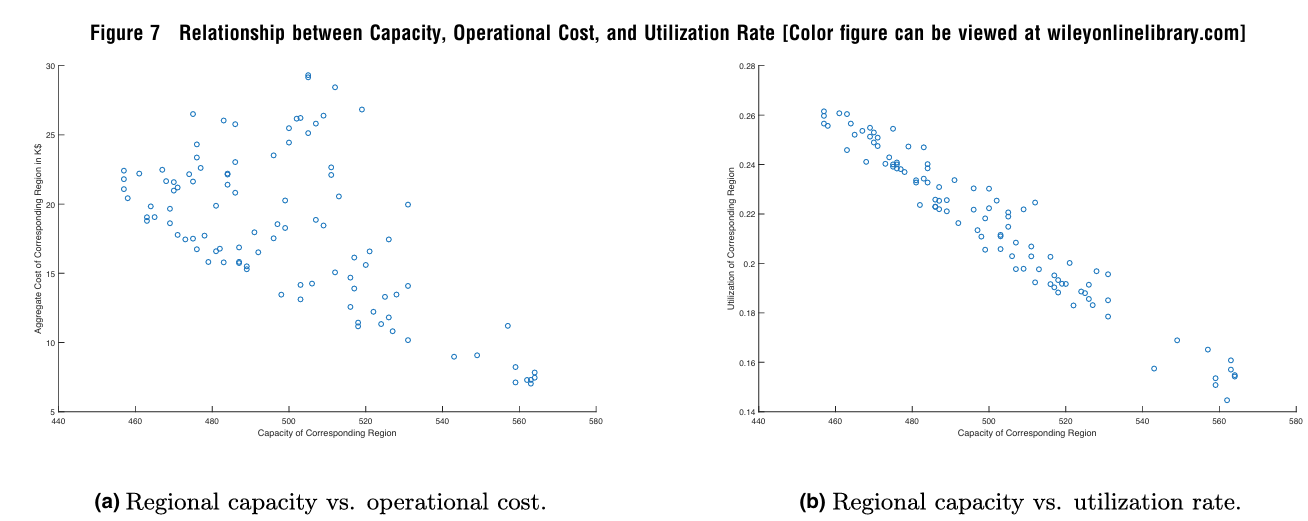
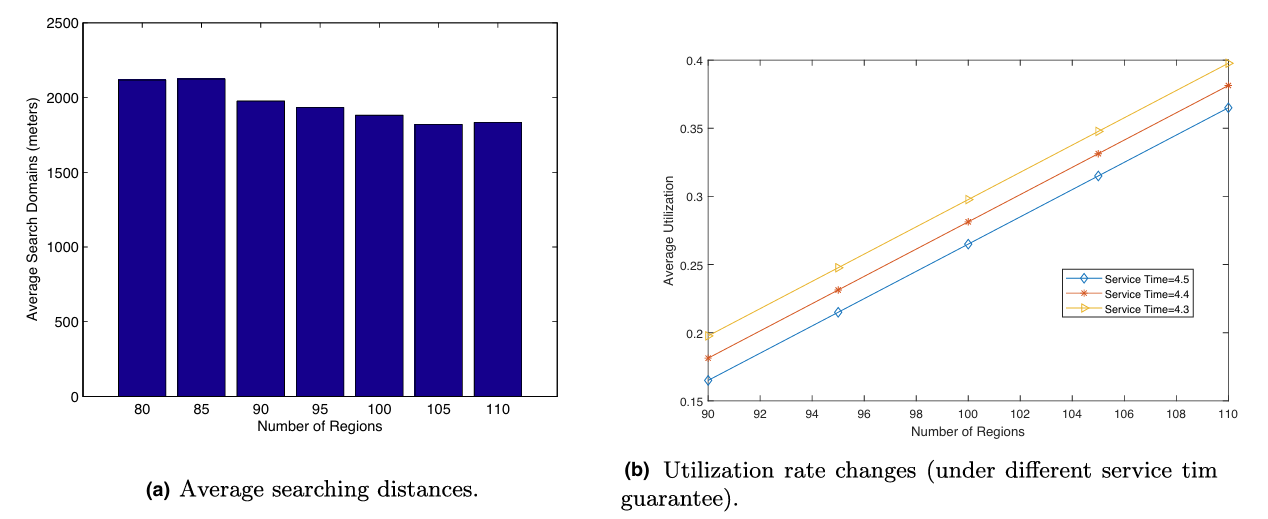
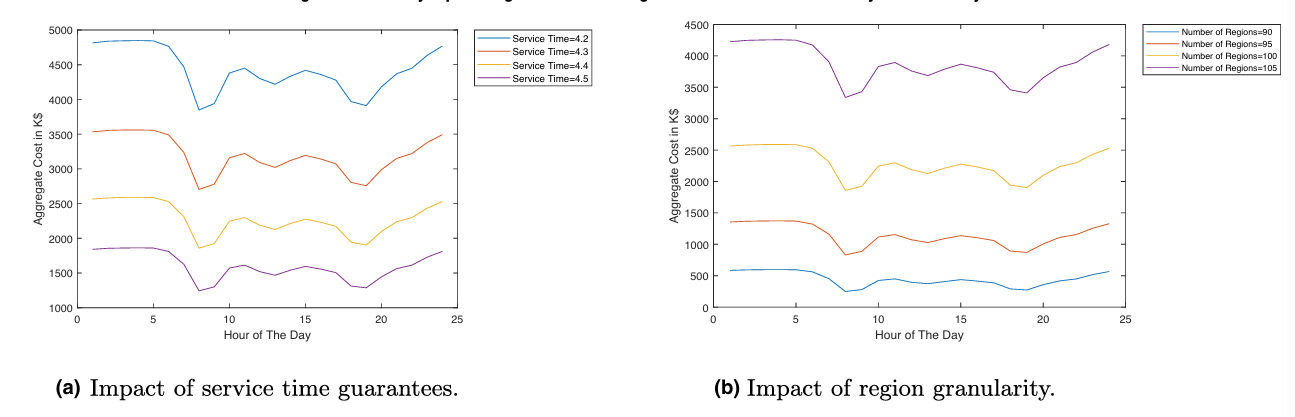
图8显示了区域划分的粒度对平均搜索距离的影响,
在图8中,平均容量利用率随着区域粒度的增加而增加,并随着服务时间保证的减少而减少。
讨论与拓展
非即时匹配
评估非零匹配时间对客户等待时间的影响。
众包 vs repositioning
当初始服务率足够高时,众包可能比重新定位更受欢迎。当运输成本(劳动力、能源和设备等)足够低时,重新定位可能更受欢迎。在我们研究的自由浮动自行车共享系统中,由于规模庞大(数百万辆自行车和连续分布的位置),与传统的站点式系统相比,重新定位的成本显著增加,使得重新定位成为一种不太理想的方法。
服务区域设计
在案例研究中,我们展示了服务区域的粒度对客户搜索域和容量利用率的关键影响。
结论
模型方面: 文章研究提出了一个基于双边匹配平台的共享出行系统综合模型,构造了一个优化问题,以确定空间容量分配和最佳的激励措施。
案例方面:在一个头部共享单车企业的数据集上进行了测试,验证了模型求解效果。
管理见解: 提出了一种使用市场力量(“众包”)而不是昂贵的repositioning的供需平衡机制。同时得到了运营成本、车辆利用率、服务水平三者之间的关系。
政策建议: 研究发现,少量的额外容量就足够了。粗粒度的服务区域划分对于平台方更为有利,因为增加了“市场厚度”。